Beregning av varmeradiatorer: hvordan beregne nødvendig antall og kraft til batterier
Et godt designet varmesystem vil gi boliger den nødvendige temperaturen, og alle rom vil være komfortable i all slags vær.Men for å overføre varme til luftrommet i boliger, må du vite det nødvendige antallet batterier, ikke sant?
Beregning av varmeradiatorer, basert på beregninger av den termiske effekten som kreves fra de installerte varmeapparatene, vil bidra til å finne ut dette.
Har du aldri gjort slike beregninger og er redd for å gjøre feil? Vi vil hjelpe deg med å forstå formlene - artikkelen diskuterer en detaljert beregningsalgoritme og analyserer verdiene til individuelle koeffisienter som brukes i beregningsprosessen.
For å gjøre det lettere for deg å forstå vanskelighetene i beregningen, har vi valgt tematiske fotografiske materialer og nyttige videoer som forklarer prinsippet om å beregne kraften til varmeenheter.
Innholdet i artikkelen:
- Forenklet beregning av varmetapskompensasjon
- Detaljert formel for beregning av termisk effekt
- Orientering av rom i henhold til kardinalretninger
- Ta hensyn til påvirkning av yttervegger
- Avhengighet av radiatorer av termisk isolasjon
- Klima er en viktig faktor i aritmetikk
- Funksjoner ved beregning av høye rom
- Designrolle for tak og gulv
- Kvaliteten på rammene er nøkkelen til varme
- Vindusstørrelsen betyr noe
- Påvirkning av lukket batteri
- Radiatortilkoblingseffektivitet
- Praktisk eksempel på beregning av termisk effekt
- Spesifikk termisk kraft til batteriseksjoner
- Beregning av antall radiatorseksjoner
- Økt varmeoverføringseffektivitet
- Konklusjoner og nyttig video om temaet
Forenklet beregning av varmetapskompensasjon
Eventuelle beregninger er basert på visse prinsipper. Beregningene av den nødvendige termiske kraften til batterier er basert på forståelsen av at velfungerende oppvarmingsenheter fullt ut må kompensere for varmetapene som oppstår under driften på grunn av egenskapene til de oppvarmede lokalene.
For stuer plassert i et godt isolert hus, plassert i sin tur i en temperert klimasone, er i noen tilfeller en forenklet beregning av kompensasjon for varmelekkasje egnet.
For slike lokaler er beregningene basert på en standardeffekt på 41 W som kreves for å varme opp 1 kubikkmeter. stue.
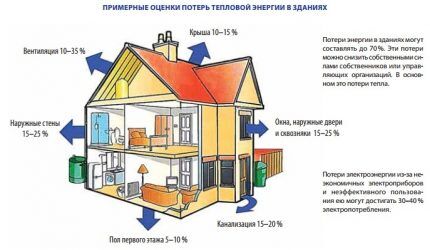
Formelen for å bestemme den termiske kraften til radiatorer som er nødvendig for å opprettholde optimale leveforhold i et rom er som følger:
Q = 41 x V,
Hvor V – volum av det oppvarmede rommet i kubikkmeter.
Det resulterende firesifrede resultatet kan uttrykkes i kilowatt, og redusere det med en hastighet på 1 kW = 1000 W.
Detaljert formel for beregning av termisk effekt
Når du gjør detaljerte beregninger av antall og størrelse på varmeradiatorer, er det vanlig å starte fra den relative effekten på 100 W som kreves for normal oppvarming av 1 m² av et visst standardrom.
Formelen for å bestemme den termiske effekten som kreves fra varmeenheter er som følger:
Q = ( 100 x S ) x R x K x U x T x H x B x G x X x Y x Z
Faktor S i beregninger, ikke noe mer enn arealet av det oppvarmede rommet, uttrykt i kvadratmeter.
De resterende bokstavene er ulike korreksjonsfaktorer, uten hvilke beregningen vil være begrenset.

Men selv ytterligere designparametere kan ikke alltid gjenspeile alle detaljene til et bestemt rom. Ved tvil om beregninger, anbefales det å foretrekke indikatorer med større verdier.
Det er lettere å da redusere temperaturen på radiatorene ved hjelp av temperaturkontrollenheterenn å fryse når deres termiske kraft er utilstrekkelig.
Deretter diskuteres hver av koeffisientene som er involvert i formelen for beregning av termisk kraft til batterier i detalj.
På slutten av artikkelen gis informasjon om egenskapene til sammenleggbare radiatorer laget av forskjellige materialer, og prosedyren for å beregne det nødvendige antall seksjoner og selve batteriene diskuteres basert på den grunnleggende beregningen.
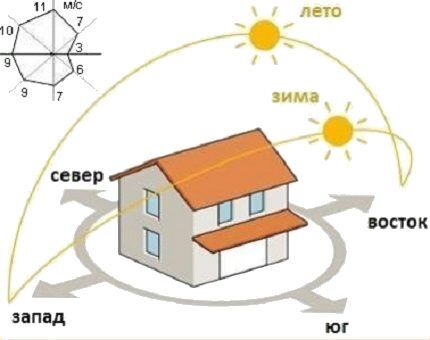
Orientering av rom i henhold til kardinalretninger
Og på de kaldeste dagene påvirker solens energi fortsatt den termiske balansen inne i hjemmet.
"R"-koeffisienten til formelen for beregning av termisk kraft avhenger av retningen til rommene i en eller annen retning.
- Rom med vindu mot sør - R = 1,0. I dagslyset vil den motta maksimal ekstern varme sammenlignet med andre rom. Denne orienteringen er tatt som den grunnleggende, og tilleggsparameteren i dette tilfellet er minimal.
- Vinduet vender mot vest - R = 1,0 eller R = 1,05 (for områder med korte vinterdager). Dette rommet vil også ha tid til å motta sin del av sollys. Selv om solen vil se ut der sent på ettermiddagen, er plasseringen av et slikt rom fortsatt gunstigere enn de østlige og nordlige.
- Rommet er orientert mot øst - R = 1,1. Den stigende vinterbelysningen vil neppe ha tid til å varme opp et slikt rom fra utsiden. Batterikraft vil kreve ekstra watt. Følgelig legger vi til en betydelig endring på 10 % i beregningen.
- Utenfor vinduet er det bare nord - R = 1,1 eller R = 1,15 (en innbygger på nordlige breddegrader vil ikke ta feil hvis han tar ytterligere 15%). Om vinteren ser ikke et slikt rom direkte sollys i det hele tatt. Derfor anbefales det å justere beregningene av varmeeffekten som kreves fra radiatorer med 10 % oppover.
Hvis vind i en bestemt retning råder i området der du bor, er det lurt for rom med vindsider å øke R med opptil 20 % avhengig av slagets styrke (x1,1÷1,2), og for rom med vegger parallelt med kalde strømmer, øk verdien av R med 10 % (x1,1).
Ta hensyn til påvirkning av yttervegger
I tillegg til veggen med vindu eller vinduer innebygd, kan også andre vegger i rommet ha kontakt med kulden ute.
Rommets ytre vegger bestemmer koeffisienten "K" til beregningsformelen for den termiske kraften til radiatorer:
- Tilstedeværelsen av én gatevegg nær et rom er et typisk tilfelle. Her er alt enkelt med koeffisienten - K = 1,0.
- To yttervegger vil kreve 20 % mer varme for å varme opp rommet - K = 1,2.
- Hver påfølgende yttervegg legger til 10 % av den nødvendige varmeoverføringen til beregningene. For tre gatevegger - K = 1,3.
- Tilstedeværelsen av fire yttervegger i et rom gir også 10 % - K = 1,4.
Avhengig av egenskapene til rommet som beregningen utføres for, må passende koeffisient tas.
Avhengighet av radiatorer av termisk isolasjon
Riktig og pålitelig isolert bolig fra vinterkulden lar deg redusere budsjettet for oppvarming av det indre rommet, og betydelig.
Graden av isolasjon av gatevegger er underlagt "U" -koeffisienten, som reduserer eller øker den beregnede termiske kraften til varmeenheter:
- U=1,0 - for standard yttervegger.
- U = 0,85 - dersom isolering av gatevegger ble utført etter en spesiell beregning.
- U = 1,27 - hvis ytterveggene ikke er kuldebestandige nok.
Vegger laget av klimaegnede materialer og tykkelse regnes som standard. Og også av redusert tykkelse, men med pusset ytre overflate eller med overflate ekstern termisk isolasjon.
Hvis området på rommet tillater det, kan du lage det isolering av vegger fra innsiden. Og det er alltid en måte å beskytte vegger mot kulden ute.

Klima er en viktig faktor i aritmetikk
Ulike klimasoner har forskjellig minimum utetemperatur.
Ved beregning av varmeoverføringseffekten til radiatorer, er det gitt en koeffisient "T" for å ta hensyn til temperaturforskjeller.
La oss vurdere verdiene til denne koeffisienten for forskjellige klimatiske forhold:
- T=1,0 opptil -20 °C.
- T=0,9 for vintre med frost ned til -15 °C
- T=0,7 – ned til -10 °C.
- T=1,1 for frost ned til -25 °C,
- T=1,3 – opptil -35 °C,
- T=1,5 – under -35 °C.
Som vi kan se av listen over, regnes vintervær ned til -20 °C som normalt. For områder med slik minst kulde tas en verdi på 1.
For varmere strøk vil denne beregningsfaktoren senke det samlede beregningsresultatet. Men for områder med tøft klima vil mengden varmeenergi som kreves fra varmeenheter øke.
Funksjoner ved beregning av høye rom
Det er klart at av to rom med samme areal, vil det med høyere tak trenge mer varme. Koeffisienten "H" bidrar til å ta hensyn til korreksjonen for volumet av oppvarmet rom ved beregning av termisk effekt.
I begynnelsen av artikkelen ble det nevnt om et visst reguleringspremiss. Dette anses å være et rom med en takhøyde på 2,7 meter eller lavere. For det, ta en koeffisientverdi lik 1.
La oss vurdere avhengigheten av koeffisienten H på takhøyden:
- H=1,0 - for tak 2,7 meter høye.
- H=1,05 - for rom opp til 3 meter høye.
- H = 1,1 - for et rom med tak opptil 3,5 meter.
- H = 1,15 – opptil 4 meter.
- H = 1,2 - varmebehov for et høyere rom.
Som du kan se, for rom med høye tak, bør 5% legges til beregningen for hver halvmeter høyde, fra 3,5 m.
I henhold til naturloven strømmer varm oppvarmet luft oppover. For å blande hele volumet, må oppvarmingsenheter jobbe hardt.

Designrolle for tak og gulv
Å redusere den termiske kraften til batterier er ikke bare bra isolerte yttervegger. Taket i kontakt med det varme rommet lar deg også minimere tap ved oppvarming av rommet.
Koeffisienten "W" i beregningsformelen er nettopp for å sørge for dette:
- W=1,0 - hvis det for eksempel er et uoppvarmet, uisolert loft oppe.
- W=0,9 - for et uoppvarmet, men isolert loft eller annet isolert rom over.
- W=0,8 - hvis rommet i etasjen over er oppvarmet.
W-indikatoren kan justeres oppover for rom i første etasje hvis de er plassert på bakken, over en uoppvarmet kjeller eller kjellerrom. Da blir tallene som følger: gulvet er isolert +20% (x1,2); gulvet er ikke isolert +40% (x1,4).
Kvaliteten på rammene er nøkkelen til varme
Vinduer var en gang et svakt punkt i den termiske isolasjonen av et oppholdsrom. Moderne rammer med doble vinduer har betydelig forbedret beskyttelsen av rom mot gatekulden.
Graden av vinduskvalitet i formelen for beregning av termisk effekt er beskrevet av koeffisienten "G".
Beregningen er basert på en standardramme med et enkeltkammer doble vinduer, hvis koeffisient er lik 1.
La oss vurdere andre alternativer for å bruke koeffisienten:
- G=1,0 - karm med en-kammer doble vinduer.
- G=0,85 - hvis karmen er utstyrt med et to- eller tre-kammer doble vinduer.
- G = 1,27 - hvis vinduet har en gammel treramme.
Så hvis huset har gamle rammer, vil varmetapet være betydelig. Derfor vil det kreves kraftigere batterier. Ideelt sett er det tilrådelig å erstatte slike rammer, fordi dette er ekstra oppvarmingskostnader.
Vindusstørrelsen betyr noe
Etter logikk kan det hevdes at jo større antall vinduer i rommet og jo bredere utsikt, desto mer følsom er varmelekkasjen gjennom dem. "X"-faktoren i formelen for å beregne den termiske effekten som kreves fra batterier, gjenspeiler dette.

Normen er resultatet av å dele arealet av vindusåpninger med arealet av rommet lik 0,2 til 0,3.
Her er hovedverdiene til X-koeffisienten for ulike situasjoner:
- X = 1,0 - i et forhold fra 0,2 til 0,3.
- X = 0,9 - for arealforhold fra 0,1 til 0,2.
- X = 0,8 - med et forhold på opptil 0,1.
- X = 1,1 - hvis arealforholdet er fra 0,3 til 0,4.
- X = 1,2 - når den er fra 0,4 til 0,5.
Hvis opptakene av vindusåpninger (for eksempel i rom med panoramavinduer) går utover de foreslåtte forholdstallene, er det rimelig å legge til ytterligere 10 % til X-verdien når arealforholdet øker med 0,1.
Døren i rommet, som regelmessig brukes om vinteren for å få tilgang til en åpen balkong eller loggia, gjør sine egne justeringer av varmebalansen.For et slikt rom vil det være riktig å øke X med ytterligere 30 % (x1,3).
Termisk energitap kan enkelt kompenseres ved kompakt installasjon av en kanalisert vann- eller elektrisk konvektor under balkonginngangen.
Påvirkning av lukket batteri
Selvfølgelig vil radiatoren som er mindre omgitt av ulike kunstige og naturlige hindringer avgi varme bedre. I dette tilfellet er formelen for å beregne dens termiske kraft utvidet på grunn av "Y" koeffisienten, som tar hensyn til driftsforholdene til batteriet.
Det vanligste stedet for oppvarmingsenheter er under vinduskarmen. I denne posisjonen er koeffisientverdien 1.
La oss vurdere typiske situasjoner for plassering av radiatorer:
- Y=1,0 - rett under vinduskarmen.
- Y = 0,9 - hvis batteriet plutselig viser seg å være helt åpent på alle sider.
- Y = 1,07 - når radiatoren er skjult av et horisontalt fremspring av veggen
- Y = 1,12 - hvis batteriet som er plassert under vinduskarmen er dekket med et frontdeksel.
- Y=1,2 - når varmeapparatet er blokkert fra alle sider.
Lange blendingsgardiner trukket ned fører også til at rommet blir kaldere.

Radiatortilkoblingseffektivitet
Effektiviteten av driften avhenger direkte av metoden for å koble radiatoren til innendørs varmeledninger. Huseiere ofrer ofte denne indikatoren for skjønnheten i rommet. Formelen for å beregne den nødvendige termiske effekten tar hensyn til alt dette gjennom "Z" koeffisienten.
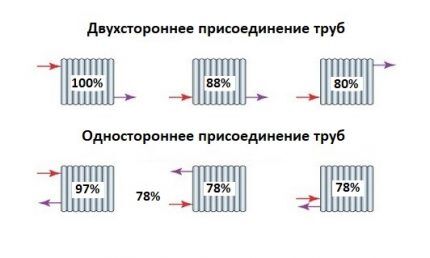
Her er verdiene til denne indikatoren for ulike situasjoner:
- Z=1,0 - koble radiatoren til den generelle kretsen til varmesystemet ved å bruke en "diagonal" metode, som er den mest berettigede.
- Z = 1,03 - en annen, mest vanlig på grunn av den korte lengden på foringen, er muligheten til å koble til "fra siden".
- Z = 1,13 - den tredje metoden er "nedenfra på begge sider". Takket være plastrør slo den raskt rot i nybygg, til tross for mye lavere effektivitet.
- Z = 1,28 - en annen, veldig ineffektiv "nedenfra på den ene siden" metode. Det fortjener kun vurdering fordi noen radiatordesign er utstyrt med ferdige enheter med både tilførsels- og returrør koblet til ett punkt.
Luftventilene installert i dem vil bidra til å øke effektiviteten til varmeenheter, noe som umiddelbart vil redde systemet fra å "lufte".
Driftsprinsippet til enhver vannoppvarmingsenhet er basert på de fysiske egenskapene til varm væske for å stige oppover og, etter avkjøling, bevege seg nedover.
Derfor anbefales det på det sterkeste å ikke bruke varmesystemkoblinger til radiatorer hvor tilførselsrøret er nederst og returrøret er øverst.
Praktisk eksempel på beregning av termisk effekt
Opprinnelige data:
- Et hjørnerom uten balkong i andre etasje i et to-etasjes pusset hus med slaggblokk i en vindstille region i Vest-Sibir.
- Romlengde 5,30 m X bredde 4,30 m = areal 22,79 kvm.
- Vindusbredde 1,30 m X høyde 1,70 m = areal 2,21 kvm.
- Romhøyde = 2,95 m.
Beregningssekvens:
| Romareal i kvm: | S = 22,79 |
| Vindusorientering – sør: | R = 1,0 |
| Antall yttervegger – to: | K = 1,2 |
| Isolering av yttervegger er standard: | U=1,0 |
| Minimum temperatur – opp til -35°C: | T=1,3 |
| Romhøyde – opptil 3 m: | H=1,05 |
| Ovenpå rommet er et uisolert loft: | W=1,0 |
| Rammer – enkeltkammer doble vinduer: | G=1,0 |
| Forholdet mellom vindu og romareal er opptil 0,1: | X = 0,8 |
| Radiatorposisjon – under vinduskarmen: | Y=1,0 |
| Radiatortilkobling – diagonalt: | Z=1,0 |
| Totalt (husk å multiplisere med 100): | Q = 2 986 watt |
Nedenfor er en beskrivelse av beregning av antall radiatorseksjoner og nødvendig antall batterier. Det er basert på de oppnådde resultatene av termisk kraft, under hensyntagen til dimensjonene til de foreslåtte installasjonsstedene til oppvarmingsenheter.
Uavhengig av resultatene, anbefales det å utstyre ikke bare vinduskarmnisjer med radiatorer i hjørnerom. Batterier bør installeres i nærheten av "blinde" yttervegger eller i nærheten av hjørner som er utsatt for den største frysing under påvirkning av gatekulde.
Spesifikk termisk kraft til batteriseksjoner
Selv før du utfører en generell beregning av den nødvendige varmeoverføringen av varmeenheter, er det nødvendig å bestemme hvilket materiale de sammenleggbare batteriene skal installeres i lokalene fra.
Valget bør være basert på egenskapene til varmesystemet (internt trykk, kjølevæsketemperatur). Samtidig, ikke glem de svært varierende kostnadene ved kjøpte produkter.
Hvordan man korrekt beregner det nødvendige antallet forskjellige batterier for oppvarming vil bli diskutert videre.
Ved en kjølevæsketemperatur på 70 °C har standard 500 mm seksjoner av radiatorer laget av forskjellige materialer ulik spesifikk termisk effekt "q".
- Støpejern - q = 160 Watt (spesifikk kraft til en støpejernsseksjon). Radiatorer fra dette metallet egnet for ethvert varmesystem.
- Stål - q = 85 Watt. Stål rørformede radiatorer kan arbeide under de tøffeste driftsforholdene. Seksjonene deres er vakre i sin metalliske glans, men har den laveste varmeoverføringen.
- Aluminium - q = 200 Watt. Lett, estetisk radiatorer i aluminium bør kun installeres i autonome varmesystemer der trykket er mindre enn 7 atmosfærer. Men deres seksjoner har ingen like når det gjelder varmeoverføring.
- Bimetall - q = 180 watt. Innmat bimetall radiatorer laget av stål, og den varmeavledende overflaten er laget av aluminium. Disse batteriene tåler alle trykk- og temperaturforhold. Den spesifikke termiske kraften til bimetallseksjoner er også høy.
De gitte verdiene av q er ganske vilkårlige og brukes til foreløpige beregninger. Mer nøyaktige tall finnes i passene til de kjøpte varmeenhetene.
Beregning av antall radiatorseksjoner
Sammenleggbare radiatorer laget av ethvert materiale er gode fordi for å oppnå sin beregnede termiske kraft, kan du legge til eller trekke fra individuelle seksjoner.
For å bestemme det nødvendige antallet "N" av batteriseksjoner fra det valgte materialet, følges formelen:
N=Q/q,
Hvor:
- Q = tidligere beregnet nødvendig termisk kraft til enheter for oppvarming av rommet,
- q = spesifikk termisk effekt av en separat seksjon av batterier foreslått for installasjon.
Etter å ha beregnet det totale nødvendige antallet radiatorseksjoner i rommet, må du forstå hvor mange batterier som må installeres. Denne beregningen er basert på en sammenligning av dimensjonene til de foreslåtte stedene installasjon av varmeapparater og batteristørrelser tatt i betraktning tilkoblingene.

For foreløpige beregninger kan du bevæpne deg med data om bredden på seksjoner av forskjellige radiatorer:
- støpejern = 93 mm,
- aluminium = 80 mm,
- bimetallisk = 82 mm.
Når du lager sammenleggbare radiatorer fra stålrør, overholder ikke produsentene visse standarder. Hvis du ønsker å installere slike batterier, bør du tilnærme deg problemet individuelt.
Du kan også bruke vår gratis online kalkulator for å beregne antall seksjoner:
Økt varmeoverføringseffektivitet
Når radiatoren varmer opp den innvendige luften i rommet, skjer det også intens oppvarming av ytterveggen i området bak radiatoren.Dette fører til ytterligere uberettigede varmetap.
For å øke effektiviteten av varmeoverføringen fra radiatoren, foreslås det å gjerde av varmeanordningen fra ytterveggen med en varmereflekterende skjerm.
Markedet tilbyr mange moderne isolasjonsmaterialer med varmereflekterende folieoverflate. Folien beskytter den varme luften som varmes opp av batteriet fra kontakt med den kalde veggen og leder den inn i rommet.
For riktig drift må grensene til den installerte reflektoren overstige radiatorens dimensjoner og stikke ut 2-3 cm på hver side. Avstanden mellom varmeanordningen og den termiske beskyttelsesflaten bør være 3-5 cm.
For å lage en varmereflekterende skjerm kan vi anbefale isospan, penofol, alufom. Et rektangel med de nødvendige dimensjonene kuttes ut av den kjøpte rullen og festes på veggen på stedet der radiatoren er installert.
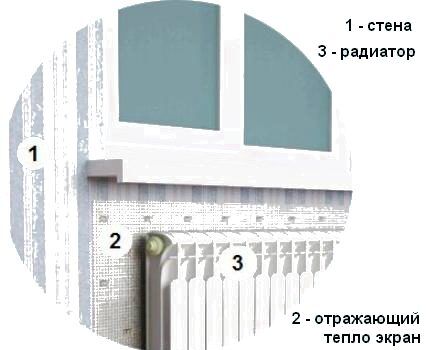
Det anbefales å skille isolasjonsplaten fra ytterveggen med en liten luftspalte, for eksempel ved hjelp av et tynt plastgitter.
Hvis reflektoren er skjøtet fra flere deler av isolasjonsmateriale, skal skjøtene på foliesiden tettes med metallisert teip.
Konklusjoner og nyttig video om temaet
Kortfilmer vil presentere den praktiske implementeringen av noen ingeniørtips i hverdagen. I den følgende videoen kan du se et praktisk eksempel på beregning av varmeradiatorer:
Endring av antall radiatorseksjoner diskuteres i denne videoen:
Følgende video vil fortelle deg hvordan du monterer reflektoren under batteriet:
De ervervede ferdighetene til å beregne den termiske kraften til forskjellige typer varmeradiatorer vil hjelpe hjemmehåndverkeren i den kompetente utformingen av varmesystemet. Og husmødre vil kunne kontrollere riktigheten av batteriinstallasjonsprosessen av tredjepartsspesialister.
Har du uavhengig beregnet kraften til varmebatterier for hjemmet ditt? Eller har du støtt på problemer som følge av installasjon av varmeenheter med lav effekt? Fortell våre lesere om opplevelsen din - legg igjen kommentarer nedenfor.




I et av rommene i leiligheten vår har utbyggerne tydelig feilberegnet - vinduet er 2,1 m langt, og radiatoren er 80 cm, og den starter tidligere, dvs. når omtrent midten av den første ventilen. Følgelig er det nesten alltid kaldt på motsatt side av vinduet, spesielt når det er vind eller frost. Varmeisolasjonsskjermen hjelper ganske bra, men vi vil fortsatt gjøre ytterligere utvendig isolasjon til våren.
Hele mitt liv bodde jeg i hus og leiligheter med støpejernsradiatorer. De var alltid brede som et vindu, jeg er så vant til det. Jeg byttet nylig ut gamle batterier med moderne enheter, og de var små, halvparten så store som et vindu, og de forsikret meg også om at dette ville være nok til oppvarming. Selvfølgelig er rommet kaldt, radiatoren kan ikke takle det. Jeg skal endre alt til våren. Hvor mye lettere var det med støpejernsradiatorer(
Hallo. Takk for detaljert informasjon.Formelen du oppga for å beregne termisk effekt inkluderer oppvarming av rommet til hvilken temperatur? Det vil si at koeffisientene til denne formelen som et resultat bare lar deg finne ut om varmetap i kilowatt, eller inkluderer formelen (koeffisientene) en reserve som vil kompensere for varmetapet og pluss sikre oppvarming av romtemperaturen til en spesifikk grad?